Suppose we have someone in a spaceship ![]() moving at some
velocity v relative to an observer
moving at some
velocity v relative to an observer ![]() . The guy in the spaceship
turns his stereo on and starts listening to some rap music!! With a
clock he measures the time interval between two beats
. The guy in the spaceship
turns his stereo on and starts listening to some rap music!! With a
clock he measures the time interval between two beats
![]() . what time interval does the
observer
. what time interval does the
observer ![]() measure? To calculate this it is easier to use the
inverse Lorentz transformations. By the Relativity principle we have:
measure? To calculate this it is easier to use the
inverse Lorentz transformations. By the Relativity principle we have:
![]()
so
![]()
But the stereo is stationary relative to ![]() so
so
![]() , so we end up with:
, so we end up with:
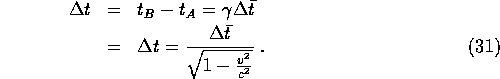
Since ![]() , time in the spaceship slows down!
That is, when the clock in the spaceship records 1 second elapsed, as
seen be the man in the ship, it shows
, time in the spaceship slows down!
That is, when the clock in the spaceship records 1 second elapsed, as
seen be the man in the ship, it shows ![]() seconds
to the man outside.
seconds
to the man outside.
The slowing of clocks in a moving system is a real effect and it applies equally to all kinds of time, for example biological, chemical reaction rates, even to the rate of growth of a cancer in a cancer patient! How is this so you may ask? If the rate of growth of the cancer was the same for a stationary patient as for a moving one, it would be possible to use the rate of cancer development to determine the speed of the ship!
A very interesting example of the slowing down of time is that
of the cosmic ray muons . These are particles
that disintegrate spontaneously after an average lifetime of about
![]() seconds. It is clear that in its short lifetime a
muon cannot, even at the speed of light, travel more than 600 m. But
although the muons are created at the top of the atmosphere,
some 10 km up, we can detect them down here on earth. How can that
be!!? From the muon's point of view (i.e.from their frame of reference) they
only live about 2
seconds. It is clear that in its short lifetime a
muon cannot, even at the speed of light, travel more than 600 m. But
although the muons are created at the top of the atmosphere,
some 10 km up, we can detect them down here on earth. How can that
be!!? From the muon's point of view (i.e.from their frame of reference) they
only live about 2 ![]() s. However from our point of view they live
considerably longer, indeed long enough to reach the surface of the
earth (by a factor of
s. However from our point of view they live
considerably longer, indeed long enough to reach the surface of the
earth (by a factor of ![]() ).
).